算法——leetcode

刷题以及快速刷题的技巧：

先掌握好数据结构以及对应的常考算法，对应着下述刷题规划网站思考+看题解；先在心里大概记忆算法和对应的示例题目，快速了解算法。

自己计算空间复杂度、时间复杂度；

算法讲解、刷题路线规划：好用网站

  1. 代码随想录
  2. labuladong算法笔记
  3. github-技术面试及刷题整理-CS-Notes

总体路线：数据结构 + 算法：经典题

算法书籍：

  1. 剑指offer 系列

算法知识点-简记

· 数据结构

  1. 数组：

    1. 特点：内存连续，查询快速，增删复杂；
    2. 算法要点：二分查找，双指针（覆盖移除、快慢双指针、左右双指针），前缀和/区间和；.sort()原地排序；
    3. 二分法：有序数组的mid中位数为界定的：排除法！！时间复杂度O(logn)

  2. 链表：单链表、双向链表、循环链表；

    1. 特点：内存不联系，查询慢速，增删容易；

    2. 算法要点：虚拟头结点、构建类（增删查改）、双指针（快n步双指针）、环形链表（数学推理）；

      1
      2
      3
      4
      class ListNode:     # 单链表
          def __init__(self, val=0, next=None):
              self.val = val
              self.next = next
      1
      2
      3
      4
      5
      class ListNode:     # 双链表
          def __init__(self, val=0, prev=None, next=None):
              self.val = val
              self.prev = prev
              self.next = next

  3. 哈希表/散列表：数组、set集合、map映射

    1. 特点：查询特别快O(1)、底层包括哈希映射+哈希碰撞；

      当需要查询一个元素是否出现过、或者一个元素是否在集合里时，第一时间想到哈希法

    2. hash table的3中结构区别：

      • 作为哈希表的数组：已知数据长度才能且最好用数组，更快（不需要哈希映射计算）；
      • 作为哈希表的set：集合，只存储key，需要哈希映射运算去计算内存地址；
      • 作为哈希表的map【dict字典】：【key-value】结构；

    3. 算法要点：先构建+再快速查询、n数和、结合双指针；

      1
      2
      3
      4
      5
      from collections import defaultdict, Counter

      dict.get(get_val, set_val_if_cannot_get)

      set() & set() # 集合相与

  4. 字符串：

    1. 算法要点：切片[::-1]、KMP前缀匹配-next前缀表O(m+n)、双指针；

      前缀表=最长公共前后缀长度表=next数组【原始、右移、减一】：j=next[index-1]

      讲解：实现strStr() KMP前缀表+next数组、prefix数组

  5. 栈与队列：

    1. 特点：
      • 栈—实现了—>递归：先进后出；出栈.pop()、查询栈顶[-1]
      • 队列：先进先出；入队.append()、查询队首[0] from collections import deque; .popleft()
      • 优先级队列=堆：大顶堆、小顶堆（完全二叉树+且树中每个结点的值都不小于（或不大于）其左右孩子的值）import heapq; heapq.heappop(pri_que)
    2. 算法要点：单调队列:push之前把前面小的删掉，队列永远是单调递减的：.pop()、单调栈【下一更大元素】时间复杂度O(n)

  6. 二叉树：

    1. 种类：

      1. 满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树
      2. 完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点
        • 所有层（除了最后一层）都完全填满。
        • 最后一层的节点尽可能靠左填充。
        • 不要求所有叶子节点在同一层。
      3. 完美二叉树、完整二叉树:
        • 所有层都完全填满。
        • 所有叶子节点都在同一层。
        • 每个非叶子节点都有两个子节点。
      4. 二叉搜索树：
        1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
        2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
        3. 它的左、右子树也分别为二叉排序树
      5. 平衡二叉树：二叉树每个节点的左右两个子树的**高度【后序遍历】**差的绝对值不超过1;

    2. 存储：

      1. 链式存储：左右指针 

        1
        2
        3
        4
        5
        class TreeNode:
            def __init__(self, val, left = None, right = None):
                self.val = val
                self.left = left
                self.right = right

      2. 顺序存储：内存是连续分布——数组

    3. 遍历：

      1. 深度优先遍历：
        • 前序遍历（递归法，迭代法用栈去实现）
        • 中序遍历（递归法，迭代法用栈去实现）
        • 后序遍历（递归法，迭代法用栈去实现）
        • 二叉树的递归3步：确定递归函数的参数和返回值–>确定终止条件–>确定单层递归的逻辑
      2. 广度优先遍历：
        • 层次遍历（迭代法用队列取实现）queue = collections.deque([root]); queue.append(); queue.popleft()

    4. 深度、高度：求深度可以从上到下去查==>前序遍历（中左右），高度只能从下到上去查==>后序遍历（左右中）

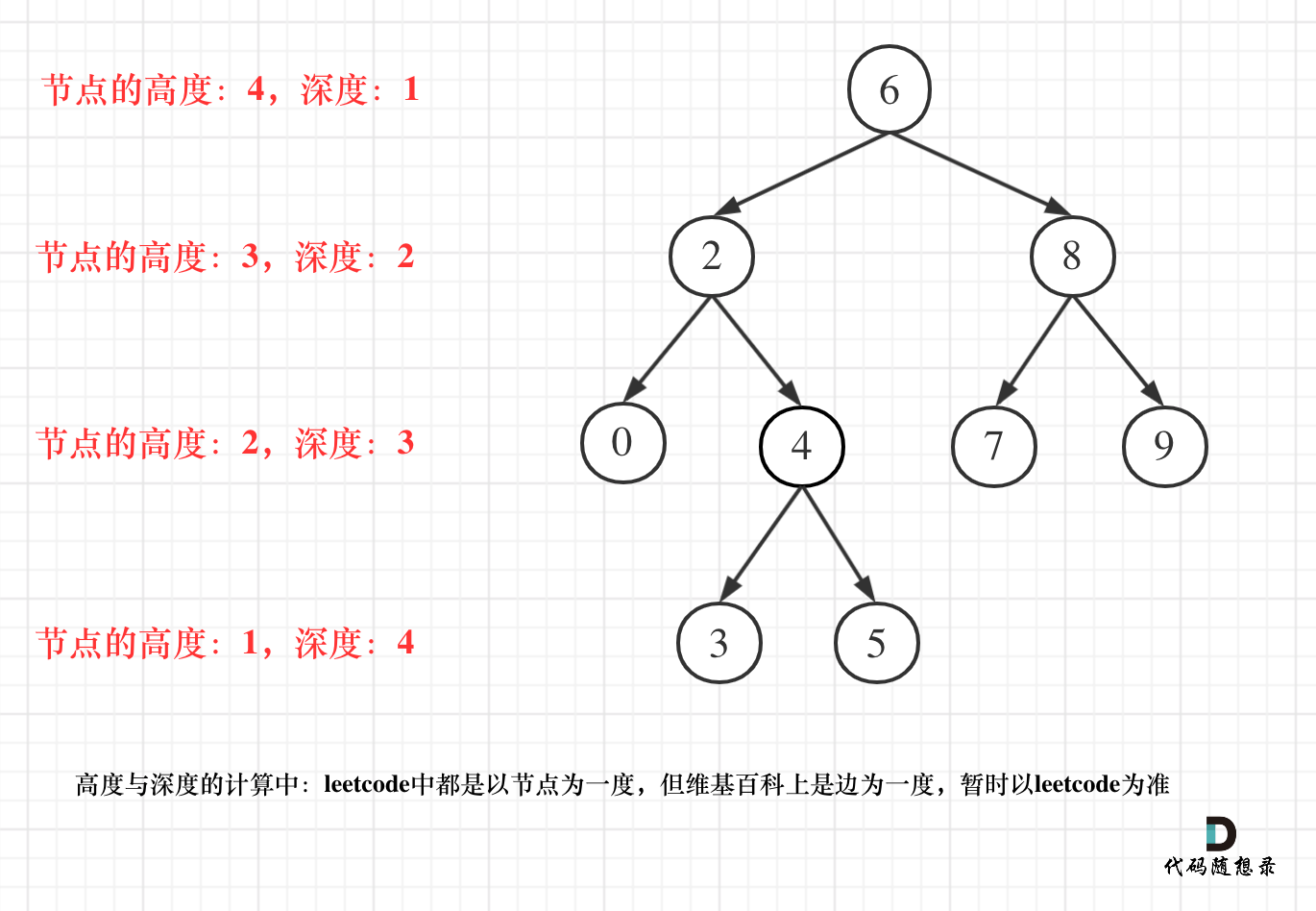
      110.平衡二叉树2

    5. 算法要点：遍历（前中后**、层序遍历**）、深度/高度、节点个数、路径【回溯】、构造与修改、公共祖先; 递归 VS 迭代 二叉树的所有路径：回溯、左叶子之和，平衡二叉搜索树BST的构建；

· 算法思想

  1. 排序

  2. 回溯

    1. 适用问题：组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

      • 组合问题：N个数里面按一定规则找出k个数的集合：
      • 切割问题：一个字符串按一定规则有几种切割方式
      • 子集问题：一个N个数的集合里有多少符合条件的子集
      • 排列问题：N个数按一定规则全排列，有几种排列方式：每层都从0开始搜索而不是startIndex、需要used数组记录已使用过元素集；
      • 棋盘问题：N皇后，解数独等等

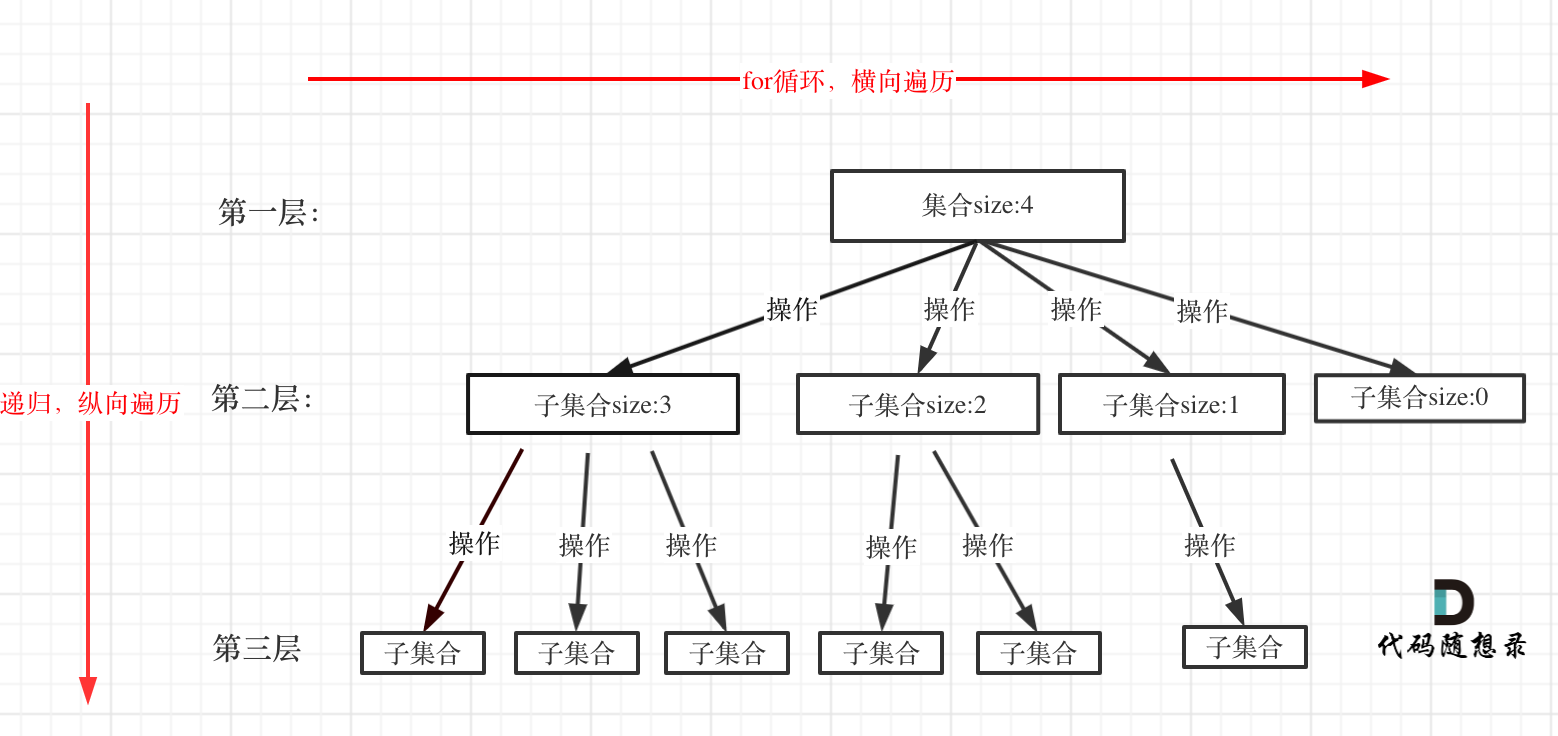
    2. 算法特点：递归（本质是穷举）回溯可以被抽象为树形结构【N叉树】；场景：在同一个/不同多个 集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。 —— “N叉树的层序遍历：for循环横向遍历，递归纵向遍历，回溯不断调整结果集。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      3步曲：
      	1. 回溯函数的模板返回值【void】以及参数
      	2. 回溯函数的终止条件
      	3. 回溯搜索的遍历过程

      void backtracking(参数) {
          if (终止条件) {
              存放结果;
              return;}
          for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
              处理节点;
              backtracking(路径，选择列表); // 递归
              回溯，撤销处理结果
          }
      }

      回溯算法理论基础

    3. 注意：

      • 集合中的元素不能重复使用时：需要startIndex调整下一层递归的起始位置；
      • 横向去重【排序后+used标记、for外used哈希表/哈希数组标记】、纵向去重[startIndex]；

  3. 贪心

    1. 特点：选择每一阶段/状态的局部最优，从而达到全局最优
    2. 经典例题：跳跃游戏、重叠区间（先排序）、发饼干

  4. 动态规划

    1. 特点：需要对前一个状态进行推导

    2. 动态规划5步曲：

      • 确定dp数组（dp table）以及下标的含义

      • 确定递推公式

      • dp数组如何初始化

      • 确定遍历顺序

      • 举例推导dp数组——打印dp数组debug

              # 动态规划：
      # 1. 结合题干-dp含义:dp
      # 2. 递归公式 
      # 3. 初始化 
      # 4. 遍历顺序
      # 5. 打印dp数组

    3. 经典例题：斐波那契、爬楼梯、整数拆分img

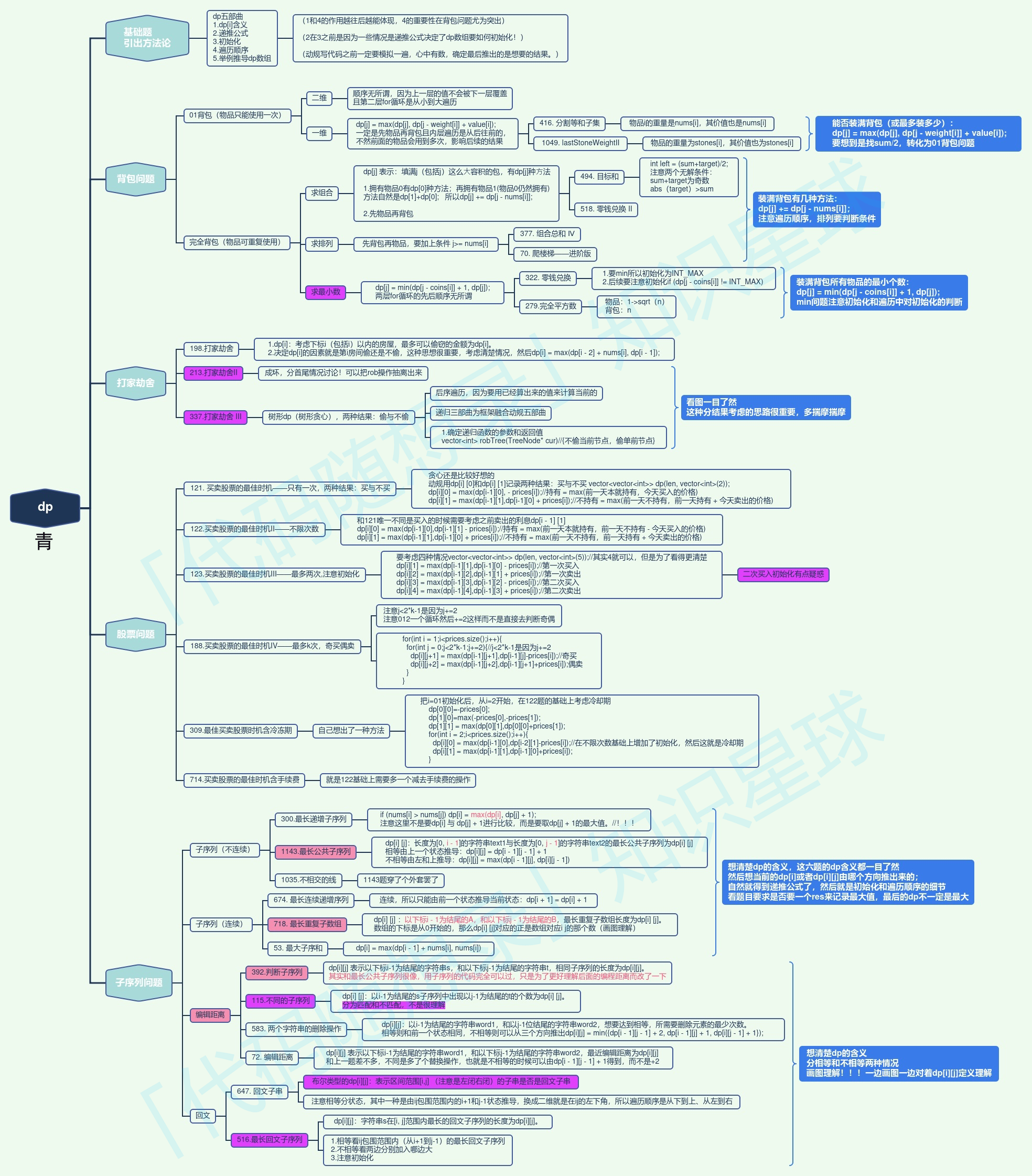
    4. 打家劫舍问题——【树形dp遍历】

    5. 股票问题——

    6. 子序列、子数组==连续子序列 问题：

          # 子序列  vs  子数组：子数组要求连续！！！
    最长公共子序列：二维dp
    # 子序列：dp[i][j]表示nums1:0~i-1 与 nums2:0~j-1的最长公共子的长度
    # 递归公式：if nums1[i-1]==nums2[j-1]:dp[i][j] = dp[i-1][j-1]+1, else: max(dp[i-1][j], dp[i][j-1])
    
    # 子数组==连续子序列：dp[i][j]表示以nums1[i-1] 与 nums2[j-1]结尾的、最长公共子数组的长度
    # 递归公式：if nums1[i-1]==nums2[j-1]:dp[i][j] = dp[i-1][j-1]+1, else:0

    7. 编辑距离问题——增删改: 二维dp数组；

    8. 回文子串问题——布尔类型的dp[i]-[j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是：dp[i]-[j]为true，否则为false

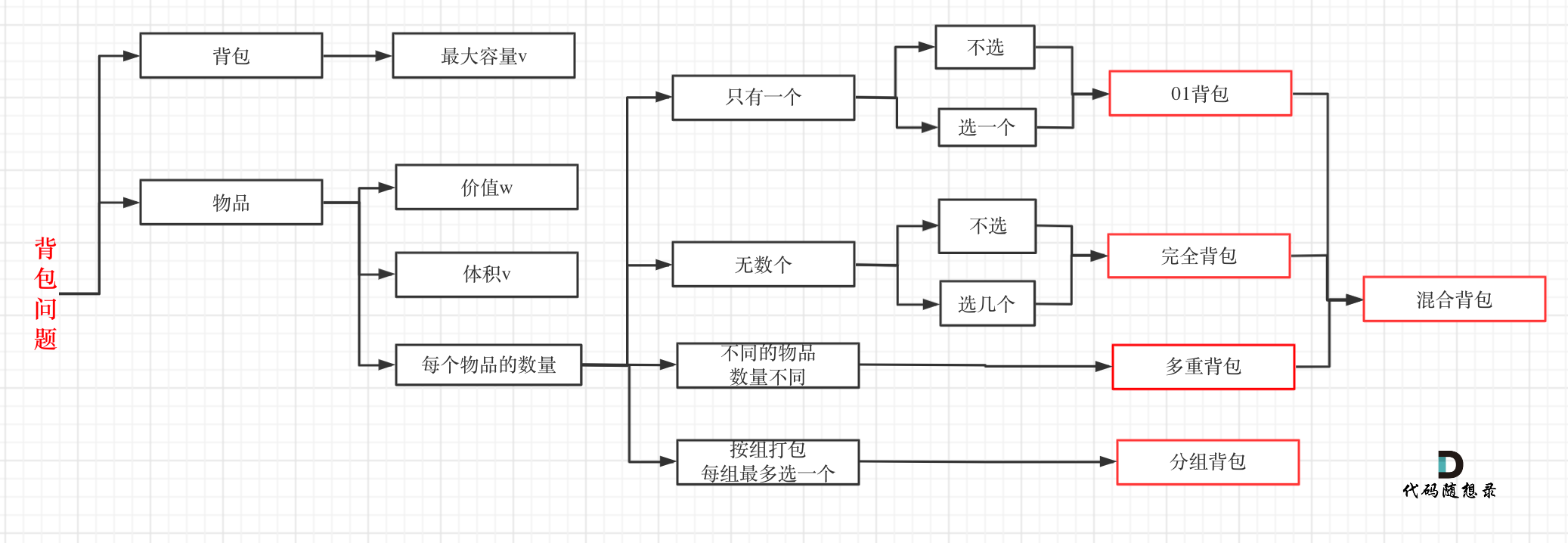
    9. 背包问题——二维dp数组 or 一维dp数组：dp[i]-[j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少：dp[i]·[j] = max( dp[ i - 1 ]·[ j ] , dp[ i - 1 ]·[ j- weight[ i ] ] + value[ i ] )

      • 01背包：一维dp数组：先物品 再倒序背包
      • 完全背包：一维dp数组：组合{先物品 再正序背包}、排列{先正序背包 再物品}

      416.背包问题-分割等和子集1

  5. 图论

LeetCode highlights
#leetcode刷题
算法——leetcode
https://pljj315.github.io/post/LeetCode-Highlights.html
作者
pljj315
发布于
2025年1月27日
许可协议